Belajar Adalah Kunci Kesuksesan: September 2012

Jumat, 28 September 2012

1. Gerak Lurus Beraturan (GLB)

Dengan rumus dasar dari definisi kelajuan, yaitu perbandingan besar perpindahan

dengan waktu tempuh

Dengan menggunakan kelajuan awal pada posisi x₀ dan waktu awal t₀= 0 maka,

Karena ∆t = t maka persamaan kelajuan di atas menjadi,

2. Gerak Lurus Berubah Beraturan (GLBB)

1. Hubungan antara kecepatan, percepatan, dan waktu

Dengan menggunakan definisi percepatan sebagai hasil bagi antara perubahan kelajuan dengan selang waktu maka kita dapatkan persamaan percepatan sebagai berikut

Dan dengan kelajuan awal v₀pada saat t0 = 0 persamaan percepatan tersebut menjadi

2. Hubungan antara perpindahan, percepatan, dan waktu

Bila kecepatan pada saat t adalah

dan perpindahan adalah kecepatan rata-rata dikali dengan waktu

dan dengan kecepatan rata-rata sendiri adalah

kita akan memperoleh sebuah persamaan:

Dengan mensubstitusikan persamaan tersebut ke dalam definisi perpindahan maka

didapatkan

3. Hubungan antara perpindahan, kecepatan, dan percepatan

Definisi waktu dari prcepatan adalah

dan jika disubstitusika ke persamaan perpindahan diperoleh

4. Hubungan antara perpindahan, kecepatan, dan waktu

Berikut ini ditampilkan beberapa contoh soal dan pembahasan dari materi Kinematika dibahas di kelas XI (11) SMA:

1) Sebuah partikel bergerak dengan persamaan posisi terhadap waktu :
r(t) =3t²−2t+1
dengan t dalam sekon dan r dalam meter.

Tentukan:

a. Kecepatan partikel saat t = 2 sekon

b. Kecepatan rata-rata partikel antara t = 0 sekon hingga t= 2 sekon

Pembahasan

a. Kecepatan partikel saat t = 2 sekon (kecepatan sesaat)

$\100dpi \\v=\frac{dr}{dt}\\v=\frac{d(3t^2-2t+1)} {dt}\\v=6t-2=6.2-2=10\,\,ms^{-1}$

b. Kecepatan rata-rata partikel saat t = 0 sekon hingga t = 2 sekon

$\100dpi \\t=2\,s\rightarrow r=3.2^2-2.2+1=9\,m\\t=0 \,s\,\rightarrow r=3.0^2-2.2+1=-3\,m\\\overline{v}=\frac{\Delta r}{\Delta t}\\\overline{v}=\frac{r_2-r_1}{t_2-t_1} \\\overline{v}=\frac{9-(-3)}{2-0}=6\,ms^{-1}$

2) Sebuah benda bergerak lurus dengan persamaan kecepatan :

$\100dpi v=[4i+(2t+2\frac{1}{3})j]\,\,ms^{-1}$

Jika posisi benda mula-mula di pusat koordinat, maka perpindahan benda selama 3 sekon adalah...
A. 10 m
B. 20 m
C. 30 m
D. 40 m
E. 50 m
(Sumber soal: Marthen Kanginan 2A, Kinematika dengan Analisis Vektor)

Pembahasan
Jika diketahui persamaan kecepatan, untuk mencari persamaan posisi integralkan persamaan kecepatan tersebut, masukkan waktu yang diminta.

$\100dpi \\x=x_o+\int_{0}^{3}vdt\\x=0+[4ti+(t^2+\frac{7}{3}t)j]^3_0=(12i+(16t)j)\\x=\sqrt{12^2+16^2}=20\,\,m\\\Delta x=x- x_0=20-0=20\,\,m$

3) Grafik kecepatan (v) terhadap waktu (t) berikut ini menginformasikan gerak suatu benda.

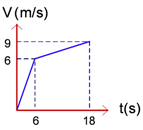
Kecepatan rata-rata benda dari awal gerak hingga detik ke 18 adalah....
A. 3 m/s.
B. 6 m/s.
C. 9 m/s.
D. 12 m/s
E. 15 m/s

Pembahasan
Kecepatan rata-rata adalah perpindahan dibagi dengan selang waktu. Jika disediakan grafik v terhadap t seperti soal diatas, perpindahan bisa dicari dengan mencari luas di bawah kurva dengan memberi tanda positif jika diatas sumbu t dan tanda negatif untuk dibawah sumbu t. Luas = perpindahan = Luas segitiga + luas trapesium

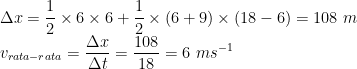
$\100dpi \\\Delta x = \frac{1}{2}\times 6\times 6 +\frac{1}{2}\times (6+9)\times (18-6)=108\,\,m\\v_{rata-rata}=\frac{\Delta x}{\Delta t}=\frac{108}{18}=6\,\,ms^{-1}$

4) Persamaan posisi sudut suatu benda yang bergerak melingkar dinyatakan sebagai berikut:

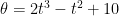
$\100dpi \\\theta =2t^3-t^2+10$

Tentukan:
a) Posisi awal
b) Posisi saat t=2 sekon
c) Kecepatan sudut rata-rata dari t = 1 sekon hingga t = 2 sekon
d) Kecepatan sudut awal
e) Kecepatan sudut saat t = 1 sekon
f) Waktu saat partikel berhenti bergerak
g) Percepatan sudut rata-rata antara t = 1 sekon hingga t = 2 sekon
h) Percepatan sudut awal
i) Percepatan sudut saat t = 1 sekon

Pembahasan
a) Posisi awal adalah posisi saat t = 0 sekon, masukkan ke persamaan posisi
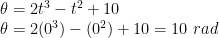
$\100dpi \\\theta =2t^3-t^2+10\\\theta = 2( 0^3)-(0^2)+10=10\,\,rad$
b) Posisi saat t = 2 sekon
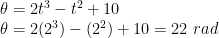
$\100dpi \\\theta =2t^3-t^2+10\\\theta = 2( 2^3)-(2^2)+10=22\,\,rad$
c) Kecepatan sudut rata-rata dari t = 1 sekon hingga t = 2 sekon
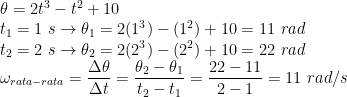
$\100dpi \\\theta =2t^3-t^2+10\\t_1=1 \,\,s\rightarrow \theta _1= 2( 1^3)-(1^2)+10=11\,\,rad\\ t_2=2 \,\,s\rightarrow \theta _2= 2( 2^3)-(2^2)+10=22\,\,rad\\\omega_{rata-rata}=\frac{\Delta \theta}{\Delta t}=\frac{\theta _2-\theta _1}{t_2-t_1}=\frac{22-11}{2-1}=11\,\,rad/s$
d) Kecepatan sudut awal
Kecepatan sudut awal masukkan t = 0 sekon pada persamaan kecepatan sudut. Karena belum diketahui turunkan persamaan posisi sudut untuk mendapatkan persamaan kecepatan sudut.
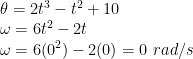
$\100dpi \\\theta =2t^3- t^2+10\\\omega = 6t^2-2t\\\omega = 6(0^2)-2(0)=0\,\, rad/s$
e) Kecepatan sudut saat t = 1 sekon
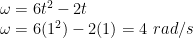
$\100dpi \\\omega = 6t^2-2t\\\omega = 6(1^2)-2(1)=4\,\, rad/s$
f) Waktu saat partikel berhenti bergerak
Berhenti berarti kecepatan sudutnya NOL.
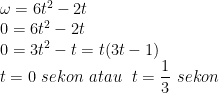
$\100dpi \\\omega = 6t^2-2t\\0 = 6t^2-2t\\0=3t^2-t=t(3t-1)\\t=0\,\,sekon \,\,atau \,\,\,\,t = \frac{1}{3}\,\,sekon$
g) Percepatan sudut rata-rata antara t = 1 sekon hingga t = 2 sekon
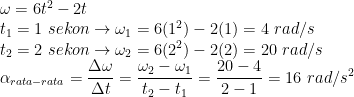
$\100dpi \\\omega = 6t^2-2t\\t_1=1\,\,sekon\rightarrow \omega_1=6(1^2)-2(1)=4\,\,rad/s\\ t_2=2 \,\,sekon\rightarrow \omega_2=6(2^2)-2(2)=20\,\,rad/s\\ \alpha_{rata-rata}=\frac{\Delta \omega}{\Delta t}=\frac{\omega_2-\omega_1}{t_2-t_1}=\frac{20-4}{2-1}=16\,\,rad/s^2$
h) Percepatan sudut awal
Turunkan persamaan kecepatan sudut untuk mendapatkan persamaan percepatan sudut.
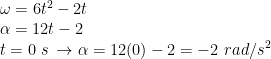
$\100dpi \\\omega = 6t^2-2t\\\alpha =12t-2\\t=0\,\,s\,\rightarrow \alpha = 12(0)-2=-2\,\,rad/s^2$
i) Percepatan sudut saat t = 1 sekon
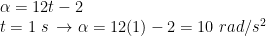
$\100dpi \\\alpha =12t-2\\t=1\,\,s\,\rightarrow \alpha = 12(1)-2=10\,\,rad/s^2$

5) Sebuah partikel bergerak dari atas tanah dengan persamaan posisi Y = (−3t² + 12t + 6 ) m/s. Tentukan :
a) Posisi awal partikel
b) Posisi partikel saat t = 1 sekon
c) Kecepatan awal partikel
d) Percepatan partikel
e) Waktu yang diperlukan partikel untuk mencapai titik tertinggi
f) Lama partikel berada di udara
g) Tinggi maksimum yang bisa dicapai partikel

Pembahasan
a) Posisi awal partikel
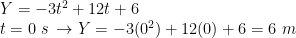
$\100dpi \\Y=-3t^2+12t+6\\t=0\,\,s\,\rightarrow Y= -3(0^2)+12(0)+6=6\,\,m$
b) Posisi partikel saat t = 1 sekon
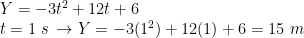
$\100dpi \\Y=-3t^2+12t+6\\t=1\,\,s\,\rightarrow Y= -3(1^2)+12(1)+6=15\,\,m$
c) Kecepatan awal partikel
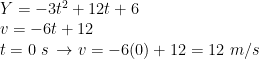
$\100dpi \\Y=-3t^2+12t+6\\v=-6t+12\\t=0\,\,s\,\rightarrow v= -6(0)+12=12\,\,m/s$
d) Percepatan partikel. Turunkan persamaan kecepatan untuk mendapatkan persamaan percepatan:
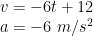
$\100dpi \\v=-6t+12\\a=-6\,\,m/s^2$
e) Waktu yang diperlukan partikel untuk mencapai titik tertinggi
Saat mencapai titik tertinggi kecepatan partikel adalah NOL.
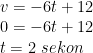
$\100dpi \\v=-6t+12\\0=-6t+12\\t=2\,\,sekon$
f) Lama partikel berada di udara
Partikel berada diudara selama dua kali waktu untuk mencapai titik tertinggi yaitu 4 sekon.
g) Tinggi maksimum yang bisa dicapai partikel
Tinggi maksimum tercapai saat 2 sekon, masukkan ke persamaan posisi.
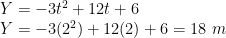
$\100dpi \\Y=-3t^2+12t+6\\Y=-3(2^2)+12(2)+6=18\,\,m$

Read more: http://fisikastudycenter.com/content/view/31/35/#ixzz160XvjnYx

Info Les Mandiri

Bimbel ICS melayani jasa bimbingan dan konsultasi belajar privat dan online untuk semua mata pelajaran dari SD-SMP-SMA/SMK.

Belajar Les mandiri di rumah, untuk bahas materi pelajaran dan PR/Tugas. Metode pengajarannya mengutamakan konsep dasar dan logika penalaran. Lebih dari itu, disertai dengan tip dan trik-trik cepat. Pengajarnya dibimbing langsung dari alumni PTN terkemuka dan guru sekolah yang sudah berpengalaman.

Untuk info lebih lanjut bisa dihubungi melalui e-mail : saliwu.aan@gmail.com

WA/Line/Instagram : 085655243352

Belajar Adalah Kunci Kesuksesan

Jumat, 28 September 2012

KINEMATIKA GERAK

soal dan pembahasan : kinematika gerak

Soal dan Pembahasan SPMB 1990-2000