Untuk melakukan pengukuran terhadap volume gas, diperlukan suatu keadaan standar untuk digunakan sebagai titik acuan. Keadaan ini yang juga dikenal sebagai STP (Standart Temperature and Pressure) yaitu keadaan dimana gas mempunyai tekanan sebesar 1 atm (760 mmHg) dan suhu °C (273,15 K).
Satu mol gas ideal, yaitu gas yang memenuhi ketentuan semua hukum-hukum gas akan mempunyai volume sebanyak 22,414 liter pada keadaan standar ini.
Hukum Gas Ideal
Definisi mikroskopik gas ideal, antara lain:
- Suatu gas yang terdiri dari partikel-partikel yang dinamakan molekul.
- Molekul-molekul bergerak secara serampangan dan memenuhi hukum-hukum gerak Newton.
- Jumlah seluruh molekul adalah besar
- Volume molekul adalah pecahan kecil yang diabaikan dari volume yang ditempati oleh gas tersebut.
- Tidak ada gaya yang cukup besar yang beraksi pada molekul tersebut kecuali selama tumbukan.
- Tumbukannya elastik (sempurna) dan terjadi dalam waktu yang sangat singkat.

Gambaran Gas Ideal
Apabila jumlah gas dinyatakan dalam mol (n), maka suatu bentuk persamaan umum mengenai sifat-sifat gas dapat diformasikan. Sebenarnya hukum Avogadro menyatakan bahwa 1 mol gas ideal mempunyai volume yang sama apabila suhu dan tekanannya sama. Dengan menggabungkan persamaan Boyle, Charles dan persamaan Avogadro akan didapat sebuah persamaan umum yang dikenal sebagai persamaan gas ideal.

atau PV = nRT
R adalah konstanta kesebandingan dan mempunyai suatu nilai tunggal yang berlaku untuk semua gas yang bersifat ideal. Persamaan di atas akan sangat berguna dalam perhitungan-perhitungan volume gas.
Nilai numerik dari konstanta gas dapat diperoleh dengan mengasumsikan gas berada pada keadaan STP, maka:
Dalam satuan SI, satuan tekanan harus dinyatakan dalam Nm-2 dan karena 1 atm ekivalen dengan 101,325 Nm-2, maka dengan menggunakan persamaan diatas dapat diperoleh harga R dalam satuan SI, sebagai berikut:

Contoh :
Balon cuaca yang diisi dengan helium mempunyai volume 1,0 x 104 L pada 1,00 atm dan 30 °C. Balon ini sampai ketinggian yang tekanannya turun menjadi 0,6 atm dan suhunya -20°C. Berapa volume balon sekarang? Andaikan balon melentur sedemikian sehingga tekanan di dalam tetap mendekati tekanan di luar.
Penyelesaian:
Karena jumlah helium tidak berubah, kita dapat menentukan n1 sama dengan n2 dan menghapusnya dari persamaan gas ideal menjadi:

Tekanan dan Suhu
Tekanan Tekanan
gas adalah gaya yang diberikan oleh gas pada satu satuan luas
dinding wadah. Torricelli (Gambar 1.17), ilmuan dari Italia yang menjadi
asisten Galileo adalah orang pertama yang melakukan penelitian tentang
tekanan gas ia menutup tabung kaca panjang di satu ujungnya dan
mengisi dengan merkuri. Kemudian ia menutup ujung yang terbuka
dengan ibu jarinya, membalikkan tabung itu dan mencelupkannya dalam
mangkuk berisi merkuri, dengan hati-hati agar tidak ada udara yang
masuk. Merkuri dalam tabung turun, meninggalkan ruang yang
nyaris hampa pada ujung yang tertutup, tetapi tidak semuanya
turun dari tabung. Merkuri ini berhenti jika mencapai 76 cm di
atas aras merkuri dalam mangkuk (seperti pada gambar dibawah).
Toricelli menunjukkan bahwa tinggi aras yang tepat sedikit beragam dari
hari ke hari dan dari satu tempat ke tempat yang lain, hal ini terjadi
karena dipengaruhi oleh atmosfer bergantung pada cuaca ditempat
tersebut. Peralatan sederhana ini yang disebut Barometer.
Tekanan
gas adalah gaya yang diberikan oleh gas pada satu satuan luas
dinding wadah. Torricelli (Gambar 1.17), ilmuan dari Italia yang menjadi
asisten Galileo adalah orang pertama yang melakukan penelitian tentang
tekanan gas ia menutup tabung kaca panjang di satu ujungnya dan
mengisi dengan merkuri. Kemudian ia menutup ujung yang terbuka
dengan ibu jarinya, membalikkan tabung itu dan mencelupkannya dalam
mangkuk berisi merkuri, dengan hati-hati agar tidak ada udara yang
masuk. Merkuri dalam tabung turun, meninggalkan ruang yang
nyaris hampa pada ujung yang tertutup, tetapi tidak semuanya
turun dari tabung. Merkuri ini berhenti jika mencapai 76 cm di
atas aras merkuri dalam mangkuk (seperti pada gambar dibawah).
Toricelli menunjukkan bahwa tinggi aras yang tepat sedikit beragam dari
hari ke hari dan dari satu tempat ke tempat yang lain, hal ini terjadi
karena dipengaruhi oleh atmosfer bergantung pada cuaca ditempat
tersebut. Peralatan sederhana ini yang disebut Barometer.
Barometer
Hubungan antara temuan Toricelli dan tekanan atmosfer dapat dimengerti berdasarkan hokum kedua Newton mengenai gerakan, yang menyatakan bahwa:
Gaya = massa x percepatan
F = m x a
Dengan percepatan benda (a) adalah laju yang mengubah kecepatan. Semua benda saling tarik-menarik karena gravitasi, dan gaya tarik mempengaruhi percepatan setiap benda. Percepatan baku akibat medan gravitasi bumi (biasanya dilambangkan dengan g, bukannya a) ialah g = 9,80665 m s-2. Telah disebutkan di atas bahwa tekanan adalah gaya persatuan luas, sehingga :
Karena volume merkuri dalam tabung adalah

Suhu
Dalam kehidupan sehari-hari kita dapat merasakan panas atau dingin. Kita bisa mendeskripsikan bahwa kutub utara mempunyai suhu yang sangat dingin atau mendeskripsikan bahwa Surabaya atau Jakarta mempunyai suhu yang panas pada siang hari. Ilustrasi diatas merupakan dua ekspresi dari suhu, akan tetapi apakah kita tau definisi dari suhu itu sendiri? Definisi suhu merupakan hal yang sepele tapi sulit untuk disampaikan tetapi lebih mudah untuk dideskripsikan. Penelitian pertama mengenai suhu dilakukan oleh ilmuan Perancis yang bernama Jacques Charles.
Campuran Gas
Pengamatan pertama mengenai perilaku campuran gas dalam sebuah wadah dilakukan oleh Dalton (Gambar 1.19), ia menyatakan bahwa tekanan total, Ptol, adalah jumlah tekanan parsial setiap gas. Pernyataan ini selanjutnya disebut sebagai Hukum Dalton, hukum ini berlaku untuk gas dalam keadaan ideal. Tekanan parsial setiap komponen dalam campuran gas ideal ialah tekanan total dikalikan dengan fraksi mol komponen tersebut.


Tekanan total dan parsial
Contoh :
Berapa tekanan total dalam wadah (container) yang mengandung:
- Metana dengan tekanan parsial 0.75 atm,
- Hidrogen dengan tekanan parsial 0.40 atm
- Propana dengan tekanan parsial 0.50 atm?
Ptot = 0.75 atm + 0.40 atm + 0.50 atm Ptot = 1.65 atm
Padatan, Cairan
Gas, cairan, dan padatan dibedakan, yang pertama atas dasar struktur fisik dan sifat kimianya(Gambar 1.21 – 1.23). Struktur fisik mempengaruhi interaksi antara partikel-partikel dan partikellingkungan. Gambaran mengenai fase gas telah diilustrasikan pada sub-bab sebelumnya. Pada sub-bab ini, pembahasan akan dititikberatkan pada fase cairan dan padatan.
Gambar Padatan

Gambar Cairan

Gambar Gas mengisi balon
Cairan
Secara umum ciri-ciri fase cairan berada diantara fase gas dan fase padat, antara lain :- Mempunyai kerapatan yang lebih tinggi bila dibanding dengan gas, namun lebih rendah bila dibandingkan dengan padatan
- Jarak antar partikel lebih dekat dekat
- Merupakan fase yang terkondensasi
- Merupakan fase yang bisa dikatakan tidak terkompresi
- Bentuk cairan akan menyesuaikan dengan wadahnya

Padatan
Sedangkan ciri-ciri fase padat, antara lain :- Kerapatannya sangat tinggi, jauh lebih tinggi daripada gas dan cairan
- Jarak antar partikel sangat dekat
- Merupakan fase yang terkondensasi
- Merupakan fase yang bisa dikatakan tidak terkompresi
- Mampu mempertahankan bentuknya


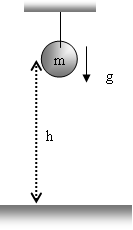
 Gambar di samping menunjukkan dua gaya
yang bekerja pada bola, yaitu gaya gravitasi
m.g dan gaya tegangan F
Gambar di samping menunjukkan dua gaya
yang bekerja pada bola, yaitu gaya gravitasi
m.g dan gaya tegangan F Gambar di samping menunjukkan permainan bola tambatan
yang dimainkan dengan cara mengikatkan sebuah bola
ke tiang dengan tali. Ketika bola dipukul, ia akan berputar
mengelilingi tiang. Kemudian yang menjadi pertanyaan,
ke arah mana percepatan bola, dan apa yang menyebabkan
percepatan itu?
Gambar di samping menunjukkan permainan bola tambatan
yang dimainkan dengan cara mengikatkan sebuah bola
ke tiang dengan tali. Ketika bola dipukul, ia akan berputar
mengelilingi tiang. Kemudian yang menjadi pertanyaan,
ke arah mana percepatan bola, dan apa yang menyebabkan
percepatan itu? Gambar di samping menunjukkan sebuah benda diikat
dengan seutas tali yang diputar membentuk lingkaran
vertikal. Bagaimanakah menentukan laju minimum bola
pada puncak lintasannya sehingga bola itu bisa terus
bergerak dalam lingkaran?
Gambar di samping menunjukkan sebuah benda diikat
dengan seutas tali yang diputar membentuk lingkaran
vertikal. Bagaimanakah menentukan laju minimum bola
pada puncak lintasannya sehingga bola itu bisa terus
bergerak dalam lingkaran?


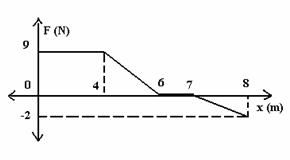
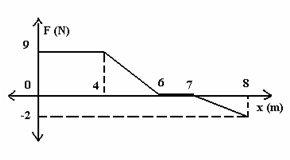

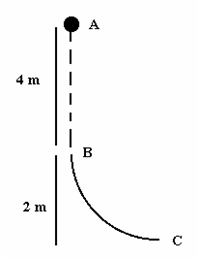

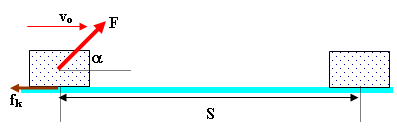
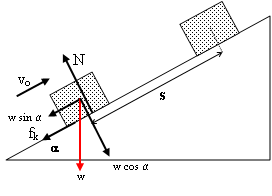
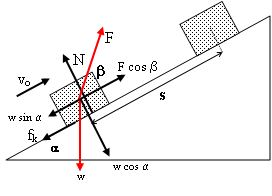
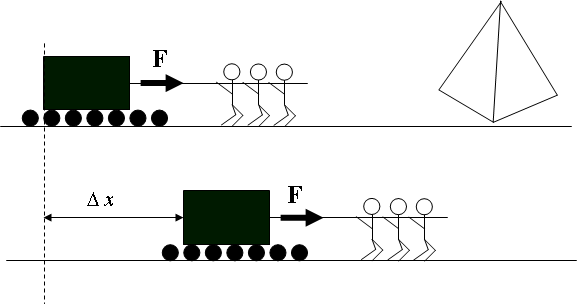

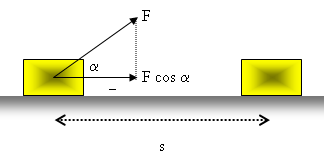
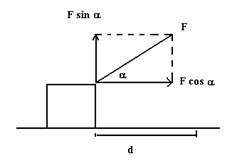
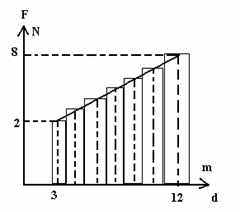 Lalu bagaimana menentukan besarnya usaha, jika gaya yang diberikan
tidak teratur. Sebagai misal, saat 5 sekon pertama, gaya yang diberikan
pada suatu benda membesar dari 2 N menjadi 8 N, sehingga benda berpindah
kedudukan dari 3 m menjadi 12 m. Untuk menentukan kerja yang dilakukan
oleh gaya yang tidak teratur, maka kita gambarkan gaya yang sejajar
dengan perpindahan sebagai fungsi jarak s. Kita bagi jarak menjadi
segmen-segmen kecil
Lalu bagaimana menentukan besarnya usaha, jika gaya yang diberikan
tidak teratur. Sebagai misal, saat 5 sekon pertama, gaya yang diberikan
pada suatu benda membesar dari 2 N menjadi 8 N, sehingga benda berpindah
kedudukan dari 3 m menjadi 12 m. Untuk menentukan kerja yang dilakukan
oleh gaya yang tidak teratur, maka kita gambarkan gaya yang sejajar
dengan perpindahan sebagai fungsi jarak s. Kita bagi jarak menjadi
segmen-segmen kecil