Soal dan Pembahasan Usaha dan Energi

1) Sebuah balok bermassa 1 kg di atas lantai licin. Jika gaya mendatar 2 N digunakan untuk menarik balok, maka tentukan usaha yang dilakukan agar balok berpindah sejauh 3 m!

Penyelesaian:

W = F . s

W = 2 . 3

W = 6 joule

2) Sebuah balok bermassa 5 kg di atas lantai licin ditarik gaya 4 N membentuk sudut 60° terhadap bidang horisontal. Jika balok berpindah sejauh 2 m, maka tentukan usaha yang dilakukan!

Penyelesaian:

W = F . s . cos a

W = 4 . 2 . cos 60°

W = 4 joule

3) Sebuah benda diberi gaya dari 3 N hingga 8 N dalam 5 sekon. Jika benda mengalami perpindahan dari kedudukan 2 m hingga 10 m, seperti pada grafik, maka tentukan usaha yang dilakukan!

Penyelesaian: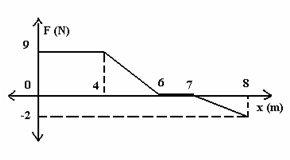

Usaha = luas trapesium

Usaha = jumlah garis sejajar x ½ . tinggi

Usaha = ( 3 + 8 ) x ½ . ( 10 – 2 )

Usaha = 44 joule

4) Buah kelapa bermassa 2 kg berada pada ketinggian 8 m. Tentukan energi potensial yang dimilikibuah kelapa terhadap permukaan bumi!

Penyelesaian:

Ep = m . g . h

Ep = 2 . 10 . 8

Ep = 160 N

5) Sebuah sepeda dan penumpangnya bermassa 100 kg. Jika kecepatan sepeda dan penumpannya 72 km/jam, tentukan energio kinetik yang dilakukan pemiliki sepeda!

Penyelesaian:

E_k = ½ . m . v² ( v = 72 km/jam = 72 x 1000 m / 3600s)

E_k = ½ . 100 . 20²

E_k = 20.000 joule

6) Sebuah pegas dengan konstanta pegas 200 N/m diberi gaya sehingga meregang sejauh 10 cm. Tentukan energi potensial pegas yang dialami pegas tersebut!

Penyelesaian:

Ep = ½ . k . Dx²

Ep = ½ . 200 . 0,1²

Ep = ½ joule

7) Suatu benda pada permukaan bumi menerima energi gravitasi Newton sebesar 10 joule. Tentukan energi potensial gravitasi Newton yang dialami benda pada ketinggian satu kali jari-jari bumi dari permukaan bumi!

Penyelesaian:

= 2,5 joule

8) Buah kelapa 4 kg jatuh dari pohon setinggi 12,5 m. Tentukan kecepatan kelapa saat menyentuh tanah!

Penyelesaian:

Kelapa jatuh memiliki arti jatuh bebas, sehingga kecepatan awalnya nol. Saat jatuh di tanah berarti ketinggian tanah adalah nol, jadi:

m.g.h₁ + ½ . m v₁² = m.g.h₂ + ½ . m . v₂²

jika semua ruas dibagi dengan m maka diperoleh :

g.h₁ + ½ .v₁² = g.h₂ + ½ . v₂²

10.12,5 + ½ .0² = 10 . 0 + ½ .v₂²

125 + 0 = 0 + ½ v₂²

v₂ =

v₂ = 15,8 m/s

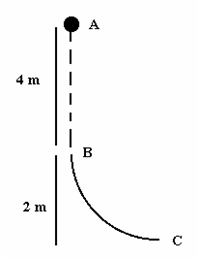
9) Sebuah benda jatuh dari ketinggian 4 m, kemudian melewati bidang lengkung seperempat lingkaran licin dengan jari-jari 2 m. Tentukan kecepatan saat lepas dari bidang lengkung tersebut!

Penyelesaian :

Bila bidang licin, maka sama saja dengan

gerak jatuh bebas buah kelapa, lintasan

dari gerak benda tidak perlu diperhatikan,

sehingga diperoleh :

m.g.h₁ + ½ . m v₁² = m.g.h₂ + ½ . m . v₂²

g.h₁ + ½ .v₁² = g.h₂ + ½ . v₂²

10.6 + ½ .0² = 10 . 0 + ½ .v₂²

60 + 0 = 0 + ½ v₂²

v₂ =

v₂ = 10,95 m/s

10) Sebuah mobil yang mula-mula diam, dipacu dalam 4 sekon, sehingga mempunyai kecepatan 108 km/jam. Jika massa mobil 500 kg, tentukan usaha yang dilakukan!

Penyelesaian:

Pada soal ini telah terdapat perubahan kecepatan pada mobil, yang berarti telah terjadi perubahan energi kinetiknya, sehingga usaha atau kerja yang dilakukan adalah :

W = ½ m v₂² – ½ m v₁²

W = ½ . 500 . 30³ – ½ . 500 . 0² ( catatan : 108 km/jam = 30 m/s)

W = 225.000 joule

11) Tentukan usaha untuk mengangkat balok 10 kg dari permukaan tanah ke atas meja setinggi 1,5 m!

Penyelesaian:

Dalam hal ini telah terjadi perubahan kedudukan benda terhadap suatu titik acuan, yang berarti telah terdapat perubahan energi potensial gravitasi, sehingga berlaku persamaan:

W = m g (h₁ – h₂)

W = 10 . 10 . (0 – 1,5)

W = – 150 joule

Tanda (– ) berarti diperlukan sejumlah energi untuk mengangkat balok tersebut.

12) Sebuah air terjun setinggi 100 m, menumpahkan air melalui sebuah pipa dengan luas penampang 0,5 m². Jika laju aliran air yang melalui pipa adalah 2 m/s, maka tentukan energi yang dihasilkan air terjun tiap detik yang dapat digunakan untuk menggerakkan turbin di dasar air terjun!

Penyelesaian:

Telah terjadi perubahan kedudukan air terjun, dari ketinggian 100 m menuju ke tanah yang ketinggiannya 0 m, jadi energi yang dihasilkan adalah :

W = m g (h₁ – h₂)

Untuk menentukan massa air terjun tiap detik adalah:

Q = A . v (Q = debit air melalui pipa , A = luas penampang , v = laju aliran air)

Q = 0,5 . 2

Q = 1 m³/s

Q = (V = volume, t = waktu, dimana t = 1 detik)

1 =

V = 1 m³

r = (r = massa jenis air = 1000 kg/m³, m = massa air)

1000 =

m = 1000 kg

W = m g (h₁ – h₂)

W = 1000 . 10 . (100 – 0)

W = 1.000.000 joule

13) Sebuah peluru 20 gram ditembakkan dengan sudut elevasi 30° dan kecepatan awal 40 m/s. Jika gaya gesek dengan udara diabaikan, maka tentukan energi potensial peluru pada titik tertinggi!

Penyelesaian:

Tinggi maksimum peluru dicapai saat vy = 0 sehingga :

v_y = v_o sin a – g .t

0 = 40 . sin 30° – 10 . t

t = 2 s

Sehingga tinggi maksimum peluru adalah :

y = v_o . sin a . t – ½ . g . t²

y = 40 . sin 30° . 2 – ½ . 10 . 2²

y = 20 m (y dapat dilambangkan h, yang berarti ketinggian)

Jadi energi potensialnya :

E_p = m . g . h (20 gram = 0,02 kg)

E_p = 0,02 . 10 . 20

E_p = 4 joule

14) Sebuah benda bermassa 0,1 kg jatuh bebas dari ketinggian 2 m ke hamparan pasir. Jika benda masuk sedalam 2 cm ke dalam pasir kemudian berhenti, maka tentukan besar gaya rata-rata yang dilakukan pasir pada benda tersebut!

Penyelesaian:

Terjadi perubahan kedudukan, sehingga usaha yang dialami benda:

W = m g (h₁ – h₂)

W = 0,1 . 10 . (2 – 0)

W = 2 joule

W = – F . s

2 = – F . 0,02 ( 2 cm = 0,02 m)

F = – 100 N

tanda (-) berarti gaya yang diberikan berlawanan dengan arah gerak benda!

15) Sebuah mobil bermassa 1 ton dipacu dari kecepatan 36 km/jam menjadi berkecepatan 144 km/jam dalam 4 sekon. Jika efisiensi mobil 80 %, tentukan daya yang dihasilkan mobil!

Penyelesaian:

Terjadi perubahan kecepatan, maka usaha yang dilakukan adalah:

W = ½ m v₂² – ½ m v₁² (1 ton = 1000 kg, 144 km/jam = 40 m/s, 36 km/jam = 10 m/s)

W = ½ 1.000 .(40)² – ½ 1.000 . (10 )²

W = 750.000 joule

P =

P =

P = 187.500 watt

h =

80 % =

P_out = 150.000 watt